A Domain-Oblivious Approach for Learning Concise Representations of Filtered Topological Spaces for Clustering
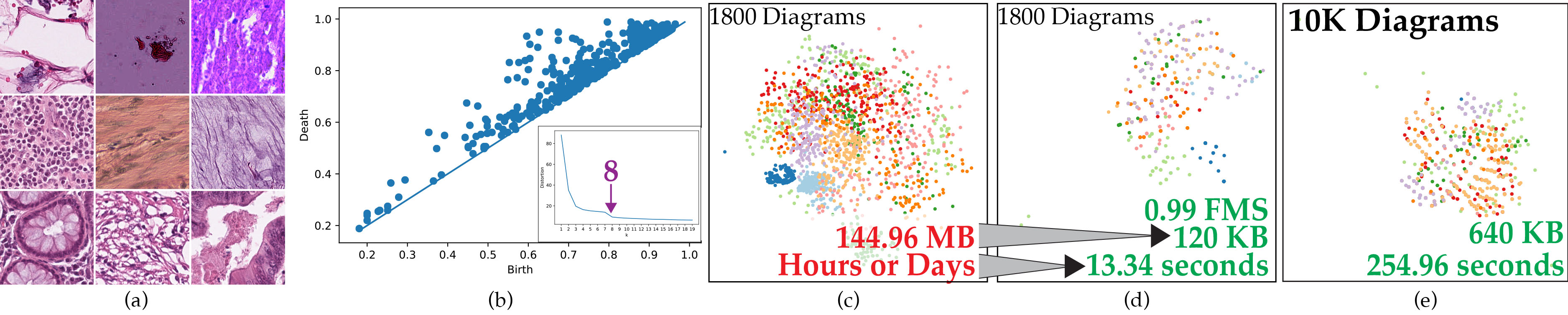 (a) Examples from a dataset of 10k histology images of colorectal cancer. (b) An example persistence diagram that encodes the topological structure in an image. The inset illustrates an elbow method plot run from clustering a subset of 1800 images using 1-Wasserstein distance. This shows there are approximately
8 topologically distinct clusters. (c) Clustering result using 1-Wasserstein distance on the subset. (d) Our high-quality concise representation uses only a fraction of the memory and computation time. (e) Our approach scales to the full dataset, which is not feasible with 1-Wasserstein.
(a) Examples from a dataset of 10k histology images of colorectal cancer. (b) An example persistence diagram that encodes the topological structure in an image. The inset illustrates an elbow method plot run from clustering a subset of 1800 images using 1-Wasserstein distance. This shows there are approximately
8 topologically distinct clusters. (c) Clustering result using 1-Wasserstein distance on the subset. (d) Our high-quality concise representation uses only a fraction of the memory and computation time. (e) Our approach scales to the full dataset, which is not feasible with 1-Wasserstein.

Demi Qin

Brittany Terese Fasy

Carola Wenk

Brian Summa
Persistence diagrams have been widely used to quantify the underlying features of filtered topological spaces in data visualization. In many applications, computing distances between diagrams is essential; however, computing these distances has been challenging due to the computational cost. In this paper, we propose a persistence diagram hashing framework that learns a binary code representation of persistence diagrams, which allows for fast computation of distances. This framework is built upon a generative adversarial network (GAN) with a diagram distance loss function to steer the learning process. Instead of using standard representations, we hash diagrams into binary codes, which have natural advantages in large-scale tasks. The training of this model is domain-oblivious in that it can be computed purely from synthetic, randomly created diagrams. As a consequence, our proposed method is directly applicable to various datasets without the need for retraining the model. These binary codes, when compared using fast Hamming distance, better maintain topological similarity properties between datasets than other vectorized representations. To evaluate this method, we apply our framework to the problem of diagram clustering and we compare the quality and performance of our approach to the state-of-the-art. In addition, we show the scalability of our approach on a dataset with 10k persistence diagrams, which is not possible with current techniques. Moreover, our experimental results demonstrate that our method is significantly faster with the potential of less memory usage, while retaining comparable or better quality comparisons.
TBD



